Вернувшись на малую родину в конце 1904 года, Эмми всё-таки официально поступила в университет, т.к. ограничения для женщин были к тому времени сняты. Изъявив желание заниматься исключительно математикой, Нётер взялась за дело с присущим ей упорством и прозорливостью: уже через 4 года она внесла значительный вклад в теорию инвариантов, успешно защитив диссертацию под руководством Пауля Гордана.

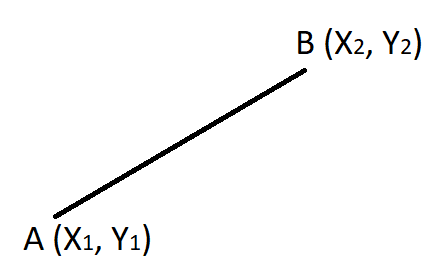
Простейший инвариант – это длина отрезка на плоскости. Если начать его вращать в любом направлении, параллельно переносить, отражать и т.д., то длина от этого не изменится. Значит, длина – это инвариант. Конечно, Эмми изучала куда более сложные вещи. 

Однако, несмотря на все трудности, в 1918 году Эмми Нётер внесла гигантский вклад... в теоретическую физику! В 36 лет она доказала теорему, названную её именем, которая связывает законы симметрии физических систем и законы сохранения энергии. 

Теорема Нётер утверждает, что каждой непрерывной симметрии физической системы соответствует некоторый закон сохранения:

• однородности времени соответствует закон сохранения энергии,
• однородности пространства соответствует закон сохранения импульса,
• изотропии пространства соответствует закон сохранения момента импульса,
• калибровочной симметрии соответствует закон сохранения электрического заряда и т. д.

Теорема обычно формулируется для систем, обладающих функционалом действия, и выражает собой инвариантность лагранжиана по отношению к некоторой непрерывной группе преобразований.

Если действие инвариантно относительно n-параметрической непрерывной группы преобразований, то существует n независимых законов сохранения.

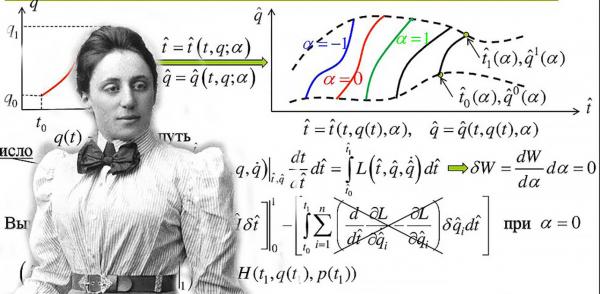
Теорема Нётер формулирует достаточное условие существования законов сохранения. Однако это условие не является необходимым, поэтому могут существовать законы сохранения, не следующие из неё (такие примеры известны). Известна теорема, формулирующая необходимые и достаточные условия существования законов сохранения.

В самой общей форме суть теоремы Нётер можно выразить буквально в двух словах. Изучая природу на фундаментальном уровне, ученые стремятся находить те характеристики физических систем, которые остаются неизменными в ходе процессов, в которых задействованы эти системы. Например, наша планета движется по своей орбите с переменной скоростью, однако воображаемый отрезок, соединяющий ее с Солнцем, за равные промежутки времени заметает равные площади (второй закон Кеплера).

Полный электрический заряд изолированной макроскопической системы не изменяется, какие бы внутренние превращения она ни претерпевала; точно так же, абсолютным постоянством отличаются и заряды элементарных частиц. Из теоремы Нётер следует, что само существование подобных сохраняющихся свойств непосредственно связано с симметриями некоторой фундаментальной физической величины, которая определяет динамику системы.

Выражаясь иначе, законы сохранения оказываются прямым следствием наличия тех или иных симметрий. Этот вывод стал самым универсальным инструментом выявления таких законов во множестве областей физики от ньютоновской механики до современной Стандартной модели элементарных частиц. Помимо этого, его можно назвать одним из наиболее красивых теоретических прозрений во всей истории науки.

Величина, о которой только что шла речь, называется действием. Ее конкретный вид зависит от системы, чье поведение она описывает. По форме это одномерный или многомерный интеграл от столь же фундаментального функционала — лагранжиана. В реальных физических процессах действие принимает экстремальное значение — чаще всего, достигает минимума. Это утверждение, не вполне точно называемое принципом наименьшего действия, позволяет с помощью методов вариационного исчисления записывать уравнения, описывающие динамику системы.